수업 목표
- 머신러닝에 대한 기본을 알고 실습환경을 구축해봅시다.
- 머신러닝의 기본! 회귀분석이 무엇인지, 평가척도는 무엇인지 알아봅시다.
- 범주형 데이터를 맞추는 분류 분석에 대해서 알아봅시다.
1. 머신러닝이란?
- 머신러닝(Machine Learning, ML)은 기술 통계 등을 통하여 집계된 정보로 의사결정을 했던 과거와 달리, 데이터 수집과 처리 기술의 발전으로 대용량 데이터의 패턴을 인식하고 이를 바탕으로 예측, 분류하는 방법론
- AI ⊃ 머신러닝 ⊃ 딥러닝
- AI : 인간의 지능을 요구하는 업무를 수행하기 위한 시스템
- Machine Learning : 관측된 패턴을 기반으로 의사 결정을 하기 위한 알고리즘
- Deep Learning : 인공신경망을 이용한 머신러닝
- Data Science : AI를 포괄하여 통계학과 컴퓨터공학을 바탕으로 발전한 융합 학문
- Data Analysis : 데이터 집계, 통계 분석, 머신러닝을 포함한 행위
- 머신러닝이 발전한 이유
: 데이터 처리 기술의 발전 -> 서비스 / 저장매체 가격의 하락
1) 머신러닝의 종류

- upervised Leaning(지도 학습)
- Unsupervised Learning(비지도 학습)
- Reinforcement Learning(강화 학습)
2) 머신러닝 적용 분야
- 금융: 신용평가, 사기탐지, 주식 예측
- 헬스케어: 질병 예측, 환자 데이터 분석
- 이커머스: 고객 구매 패턴 분석, 추천 시스템, 가격 최적화, 장바구니 분석
- 자연어처리: 번역, 챗봇, 텍스트분석
- 이미지 & 영상처리: 얼굴인식, 이미지 생성
3) 머신러닝 실습 소프트웨어
|
2. 회귀분석 - 선형회귀
- 방정식을 배운 머신이는 몸무게와 키의 데이터를 획득했다. 일정하게 증가하는 패턴이 있어서 미리 몸무게를 알면 키를 알 수 있을 것이라고 생각했다.
 |
 |
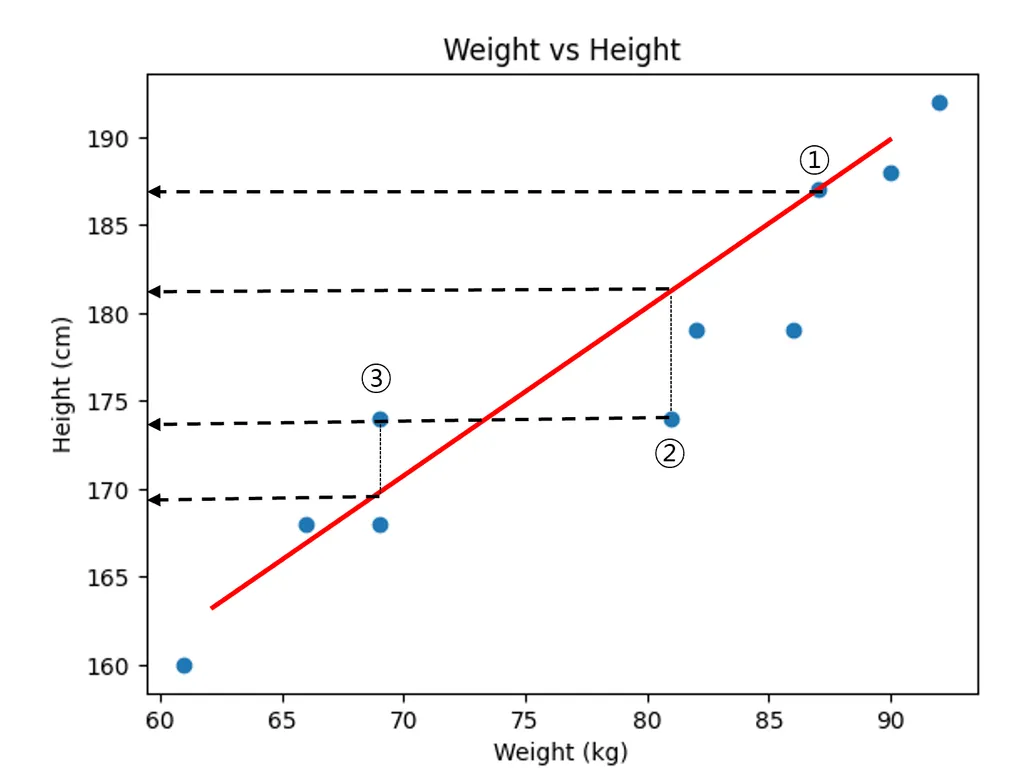
- 머신이는 3개의 그래프를 그려보니, 아무래도 초록색, 파란색 직선보다는 빨간색 그래프가 적절한 것 같다. 하지만 이렇게 대강 직선을 그리다 보면 적절한 그래프를 찾기 어려울 것 같아 고민이 빠졌다.
- 머신이는 하나의 생각을 떠 올렸다. 바로 직선과 점의 간의 거리를 계산하는 것이다. 이를 Error 라고 정의하고 최소의 Error인 직선을 그리면 된다고 생각했다.
- 방법1) 실제 데이터 값 - 직선의 예측 값 = Error
- 문제1) 선분을 기준으로 위에 있는 데이터 거리를 계산하면 양수가 되고, 반대로 아래에 있는 것은 음수가 된다. 이 경우 모든 에러를 합치면 서로 상쇄. 따라서, 음수를 양수로 만들기 위해 제곱.
- 방법2) 각각 Error를 제곱하여 모두 더하기
- 문제2) 데이터 추가시, 데이터가 늘어날 수록 에러는 값이 커질 수 밖에 없으므로 데이터의 개수로 나눔. 또한, 데이터가 제곱이 되어 있던 것을 줄이기 위해 루트를 씌우기로 함.
- 방법3) 전체 에러 합에 데이터의 개수로 나누기
- 방법1) 실제 데이터 값 - 직선의 예측 값 = Error
 |
 |
 |
1) 선형회귀 용어 정리
- Y는 종속 변수, 결과 변수
- X는 독립 변수, 원인 변수, 설명 변수
- 통계학에서 사용하는 선형회귀 식
- Y = β₀ + β₁X + ε
- β₀ : 편향(Bizs) / β₁ : 회귀계수 / ε : 오차(에러), 모델이 설명하지 못하는 Y의 변동성
2) 회귀분석의 평가지표
- MSE(Mean Squared Error, 평균 제곱 오차)
- 방법1) 에러 = 실제 데이터 - 예측 데이터로 정의하기
- 방법2) 에러를 제곱하여 모두 양수로 만들기, 다 합치기
- 방법3) 데이터만큼 나누기
 |
 |
 |
- RMSE : MSE에 Root를 씌워 제곱 된 단위를 다시 맞추기
- MAE : 절댓값을 이용하여 오차 계산하기
 |
 |
- R Square
: 전체 모형에서 회귀선으로 설명할 수 있는 정도

3) 다중 선형회귀

4) 수치형 데이터 vs 범주형 데이터
- 수치형 데이터
- 연속형 데이터 : 두 개의 값이 무한한 개수로 나누어진 데이터 (키, 몸무게)
- 이산형 데이터 : 두 개의 값이 유한한 개수로 나누어진 데이터 (주사위 눈, 나이)
- 범주형 데이터
- 순서형 자료 : 자료의 순서 의미가 있음 (학점, 등급)
- 명목형 자료 : 자료의 순서가 의미가 없음 (혈액형, 성별)
5) 회귀 실습
(1) 범주형 데이터 인코딩
 |
 |
(2) 훈련 & 학습

(3) 예측

(4) 평가

6) 선형회귀 정리
- 선형회귀의 가정
- 선형성(Linearity) : 종속 변수(Y)와 독립 변수(X) 간에 선형 관개가 존재해야 함.
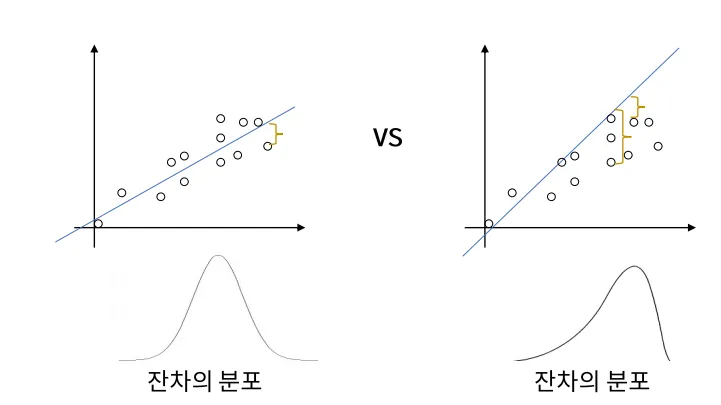
- 등분산성(Homoscedasticity) : 오차의 분산이 모든 수준의 독립 변수에 대해 일정해야 함. 즉, 오차가 특정 패턴을 보여서는 안 되며, 독립 변수의 값에 상관없이 일정해야 함.
- 정규성(Normality) : 오차 항은 정규 분포를 따라야 함.
- 독립성(Independence) : X 변수는 서로 독립적이야 함.
 |
 |
 |
- 다중공선성 문제
- 변수가 많아지면 서로 연관이 있는 경우가 많아지고, 이처럼 회귀분석에서 독립변수(X) 간의 강한 상관관계가 나타나는 것을 다중공선성(Multicolinearity) 문제라고 한다.
- 서로 상관관계가 높은 변수 중 하나만 선택(산점도 혹은 상관관계 행렬
- 두 변수를 동시에 설명하는 차원축소(Principle Component Analysis, PCA)를 실행하여 변수 1개로 축소
 |
 |
 |
- 선형회귀의 장점
- 직관적이며 이해하기 쉽다. X-Y 관계를 정량화 할 수 있다.
- 모델이 빠르게 학습된다.(가중치 계산이 빠르다)
- 선형회귀의 단점
- X-Y 간의 선형성 가정이 필요하다.
- 평가지표가 평균(mean) 포함 하기에 이상치에 민감하다.
- 범주형 변수를 인코딩시 정보 손실이 일어난다.
- 선형회귀 숙제
3. 분류분석 - 로지스틱회귀
1) 로지스틱 함수
- 범주형 Y에서 선형함수의 한계 - X가 연속형 변수이고, Y가 특정 값이 될 확률이라고 설정한다면, 왼쪽 그림과 같이 선형으로 설명하기 어려운 경우가 생긴다. 확률은 0과 1 사이인데, 예측 값이 확률 범위를 넘어갈 수 있음.

-
- 오즈비(odds ratio)는 실패확률 대비 성공 확률로, 도박사들이 자주 쓰는 개념
- 도박이 성공할 확률이 80%라면, 오즈비는 80% / 20% = 4, 1번 실패하면 4번은 딴다.
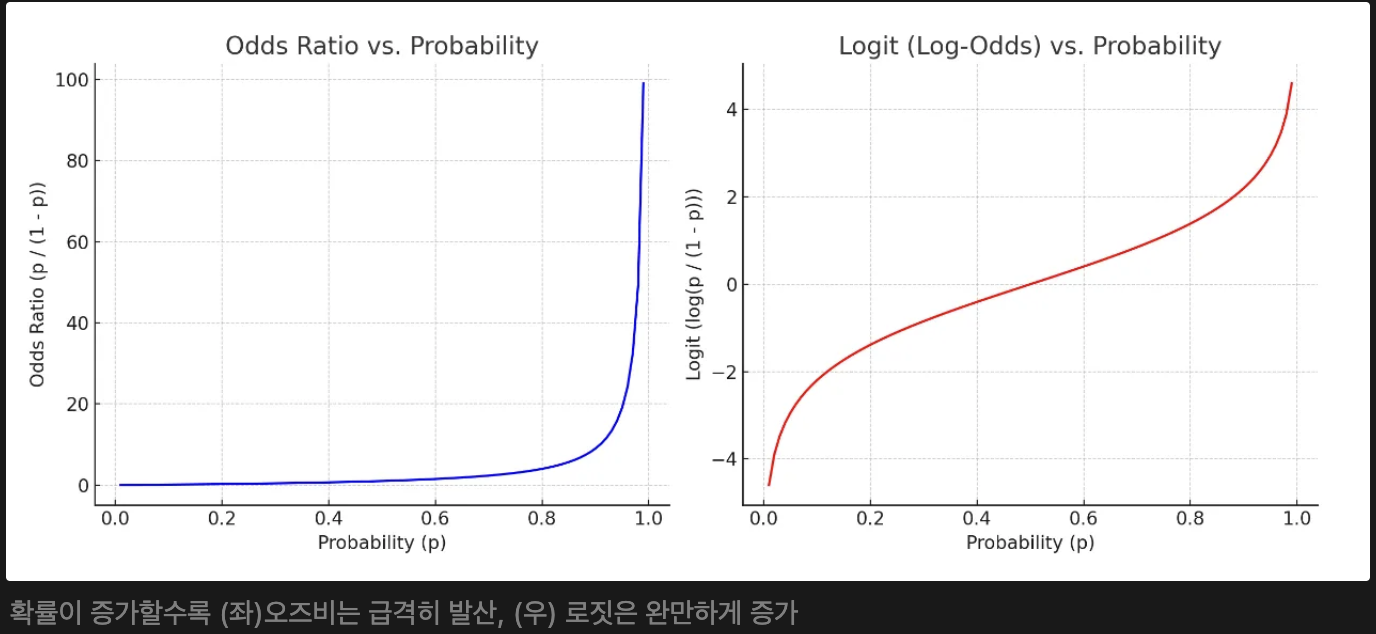
- 오즈비(odds ratio) = P / (1-P)
- P는 확률 값으로 0과 1 사이인데, P가 증가할수록 오즈비가 급격하게 증가하기 때문에 너무 확률이 급격히 등가하고 선형성을 따르지 않게 되므로 로그를 써서 이를 완화
- Logit = log(P / (1-P) )
- 오즈비보다 로짓의 그래프가 더 선형적인 그림을 나타내어 선형회귀의 기본식을 활용할 수 있게 됨
- 분류 모델임에도 로지스틱"회귀"라고 불리는 이유가 이것
- 로지스틱 함수 - 시그모이드 함수 중 하나로 값을 계산하면 확률이 도출된다.

- 로짓의 장점은 어떤 값을 가져오더라도 반드시 특정 사건이 일어날 확률(Y 값이 특정 값일 확률)이 0과 1로 들어오게 하는 특징을 갖음

- 로지스틱 함수는 가중치 값을 안다면 X 값이 주어졌을 때 해당 사건이 일어날 수 있는 P의 확률 계산 가능
- 확률 0.5를 기준으로 그보다 높으면 사건이 일어남(P(Y)=1), 그렇지 않으면 사건이 일어나지 않음(P(Y)=0)으로 판단하여 분류 예측에 사용
2) 분류 평가 지표
- 정확도와 F1-Score
- 정확도의 한계
- 예측 모델: 무조건 환자가 음성(정상인)이라고 판정
- 100명의 환자 입실, 95명은 음성(정상), 5명은 양성(암 환자)
- 위에 따르면 암 예측 모델의 정확도는 95%
- 정확도는 매우 높아 보이지만, 실제로 양성(암 환자)는 하나도 맞추지 못 함
- 혼돈행렬(Confusion Matrix) - 실제 값과 예측 값에 대한 모든 경우의 수를 표현하기 위한 2X2 행렬

- 표기법
- 실제와 예측이 같으면 True / 다르면 False
- 예측을 양성으로 했으면 Positive / 음성으로 했으면 Negative
- 해석
- TP: 실제로 양성(암 환자)이면서 양성(암 환자) 올바르게 분류된 수
- FP: 실제로 음성(정상인)이지만 양성(암 환자)로 잘못 분류된 수
- FN: 실제로 양성(암 환자)이지만 음성(정상인)로 잘못 분류된 수
- TN: 실제로 음성(정상인)이면서 음성(정상인)로 올바르게 분류된 수
- 지표
1. 정밀도(Precision): 모델이 양성 1로 예측한 결과 중 실제 양성의 비율(모델의 관점) |
2. 재현율(Recall): 실제 값이 양성인 데이터 중 모델이 양성으로 예측한 비율(데이터의 관점) |
3. f1-Score: 정밀도와 재현율의 조화 평균 |
4. 정확도(Accuracy) |
3) 로지스틱회귀 정리
- 장점 : 직관적이며 이해가 쉽다.
- 단점 : 복잡한 비선형 관계를 모델링하기 어려울 수 있다.
4. 모델링 기본 마무리
- 선형회귀와 로지스틱회귀의 공통점
- 모델 생성이 쉬움
- 가중치(혹은 회귀계수)를 통한 해석이 쉬운 장점이 있음
- X 변수에 범주형, 수치형 변수 둘 다 사용 가능
- 선형회귀와 로지스틱 분류 차이점

- 실제로 데이터의 모델링은 데이터 사이언스 업무의 아주 일부분이며, 대부분 데이터의 수집과 전처리에 아주 많은 시간을 쓰게 된다.
- 전체 데이터 분석 프로세스

'내일배움캠프_QAQC 트랙 1기 > 강의 요약' 카테고리의 다른 글
| [내일배움캠프] 머신러닝의 이해와 라이브러리 활용 심화 2주차 (0) | 2025.02.21 |
|---|---|
| [내일배움캠프] 머신러닝의 이해와 라이브러리 활용 심화 1주차 (0) | 2025.02.19 |
| [내일배움캠프] 통계학 기초 3주차 (3) | 2025.01.21 |
| [내일배움캠프] 통계학 기초 2주차 (3) | 2025.01.17 |
| [내일배움캠프] 통계학 기초 1주차 (2) | 2025.01.16 |